常见算法的C语言实现(带题目、分析和答案) 穷举 递归 迭代 递推 分治 回溯 动态规划 贪心
1.1 基本思想
1.1.1 穷举
穷举(又称枚举)算法的基本思想是从所有可能的情况中搜索正确的答案。
a) 题一
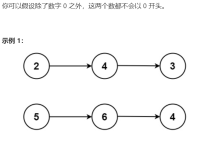
查找数组中的两个元素,它们的和等于给定的目标值。给定一个包含 n 个整数的数组和一个目标值,找出数组中是否存在两个元素,它们的和等于目标值。如果存在,返回这两个元素的索引,如果不存在,返回一个特殊值(如-1)。
思路:
穷举所有可能的组合: 使用两层循环遍历数组的所有元素组合。
判断是否满足条件: 对于每一对元素,判断它们的和是否等于目标值。
返回结果: 如果找到满足条件的组合,返回它们的索引;否则,返回特殊值。
解:
#include <stdio.h>
// 穷举法查找数组中两个元素的和等于目标值的索引
void findTwoElements(int arr[], int size, int target) {
// 遍历数组的所有元素组合
for (int i = 0; i < size - 1; i++) {
for (int j = i + 1; j < size; j++) {
// 判断是否满足条件
if (arr[i] + arr[j] == target) {
// 找到满足条件的组合,输出索引
printf("找到元素:%d + %d = %d,索引:%d 和 %d\n", arr[i], arr[j], target, i, j);
return;
}
}
}
// 没有找到满足条件的组合
printf("没有找到满足条件的组合\n");
}
int main() {
// 示例数组
int arr[] = {2, 7, 11, 15};
// 目标值
int target = 9;
// 数组的大小
int size = sizeof(arr) / sizeof(arr[0]);
// 使用穷举法查找数组中两个元素的和等于目标值的索引
findTwoElements(arr, size, target);
return 0;
}
1.1.2 递归
递归调用是一个方法在其方法体内调用其自身方法。
b) 题一

解1(推导法):
在f函数中,当输入的x大于0时,返回x*f(x-1),当x等于0时,返回2。
可将f看做An,且A0=2。An=n*A(n-1);则An/A(n-1)=n;则An=2*!n,(n>=1)
则f(f(1)=4。
解2(带值法):
在f函数中,当输入的x大于0时,返回x*f(x-1),当x等于0时,返回2。
例如输入0,则f返回2。输入1,f返回1*f(1-1)=1*2=2。输入2,则返回2*f(2-1)=2*2=4。
对于i=f(f(1)),从内开始看,f(1)=2,则结果等价于f(2),即等于4。
c) 题二
编写计算斐波那契(Fibonacci)数列的函数,数列大小为n。无穷数列1,1,2,3,5,8,13,21,35,…,称为斐波那契数列。这种数列有一个规律,数列第1个与第2个元素的值均为1,从第3个值开始,每个数据是前两个数据之和。
解:
数列可以表示为:
1,1,(1+1),(1+(1+1)),((1+1)+(1+(1+1)))…
在此,我们可以把这种规律转成递推式:

有了递推式,再来写程序,也就很容易了,直接转化即可,该问题程序实现如下所示:

1.1.3 迭代
很多时候无法使用公式一次求解,当使用迭代法时,通常是通过反复应用某种规则或算法来逐步逼近问题的解。
a) 题一
给定一个非负整数,请使用加减乘除和循环语句实现算法,计算其平方根并返回,只保留整数部分即可。
思路:
选择初始解: 使用给定的数作为初始解。
迭代更新: 反复应用迭代公式,逐步逼近平方根。
判断停止条件: 当迭代结果满足停止条件时,返回结果。
解:
#include <stdio.h>
// 迭代法计算平方根
int sqrtIteration(int x) {
if (x == 0 || x == 1) {
return x;
}
// 初始化解为 x/2
int result = x / 2;
// 迭代更新
while (result > x / result) {
result = (result + x / result) / 2;
}
return result;
}
int main() {
// 示例输入
int x = 25;
// 使用迭代法计算平方根
int result = sqrtIteration(x);
// 输出结果
printf("数字 %d 的平方根为 %d\n", x, result);
return 0;
}
1.1.4 递推
递推算法是一种理性思维模式的代表,其根据已有的数据和关系,逐步推导而得到结果。
a) 题一
递推和递归的区别?
递推:
计算方式: 递推是一种迭代的计算方式,通过定义初始项和递推关系,从初始项开始逐步计算出目标项。
实现方式: 通常使用循环结构,从初始项开始,通过迭代计算得到目标项。
特点: 递推是一种自底向上的计算方式,从已知的初始项逐步推导出后续项,不涉及函数调用栈的压栈和弹栈过程。
递归:
计算方式: 递归是一种通过将问题分解为更小规模的相同问题来解决的方式,通过递归调用自身来计算目标项。
实现方式: 通常通过函数的递归调用来实现,每次调用解决一个更小规模的问题,直到达到基本情况。
特点: 递归是一种自顶向下的计算方式,通过将大问题分解为小问题,通过递归调用逐步解决小问题,并将结果合并。
区别总结:
递推是迭代的,递归是通过函数调用实现的。
递推从初始项开始迭代计算,自底向上;递归通过不断将问题分解,自顶向下。
递推通常使用循环结构,递归使用函数调用。
b) 题二
计算斐波那契数列。
思路:
定义初始项: 斐波那契数列的前两项为 0 和 1。
递推关系: 第 n 项等于前两项的和,即 F(n) = F(n-1) + F(n-2)。
递推计算: 使用循环或递归,依次计算出第 n 项的值。
解:
#include <stdio.h>
// 递推法计算斐波那契数列的第 n 项
int fibonacci(int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
}
// 定义初始项
int fib0 = 0;
int fib1 = 1;
// 递推计算
for (int i = 2; i <= n; i++) {
int temp = fib1;
fib1 = fib0 + fib1;
fib0 = temp;
}
return fib1;
}
int main() {
// 示例输入
int n = 7;
// 使用递推法计算斐波那契数列的第 n 项
int result = fibonacci(n);
// 输出结果
printf("斐波那契数列的第 %d 项为 %d\n", n, result);
return 0;
}
1.1.5 分治
分治算法的基本思想是将一个计算复杂的问题分成规模较小、计算简单的小问题求解,然后综合各个小问题,得到最终答案。
归并排序体现的便是分治的思想,将大问题分成小问题,并进行解决。
a) 题一
给定一个包含 n 个元素的数组,设计一个分治算法,找到数组中的最大元素及其索引。
思路:
基本情况: 如果数组中只有一个元素,那么该元素即为最大元素。
分解问题: 将数组分为两半,分别在左半部分和右半部分递归查找最大元素。
合并结果: 比较左右两半部分找到的最大元素,返回较大者。
解:
#include <stdio.h>
// 定义结构体表示包含最大元素及其索引的结果
struct MaxResult {
int maxElement;
int maxIndex;
};
// 分治算法函数,查找数组中的最大元素及其索引
struct MaxResult findMax(int arr[], int start, int end) {
struct MaxResult result;
// 基本情况:只有一个元素
if (start == end) {
result.maxElement = arr[start];
result.maxIndex = start;
return result;
}
// 分解问题:将数组分为两半
int mid = (start + end) / 2;
// 递归查找左半部分的最大元素
struct MaxResult leftResult = findMax(arr, start, mid);
// 递归查找右半部分的最大元素
struct MaxResult rightResult = findMax(arr, mid + 1, end);
// 合并结果:比较左右两半部分找到的最大元素
if (leftResult.maxElement > rightResult.maxElement) {
return leftResult;
} else {
return rightResult;
}
}
int main() {
// 示例数组
int arr[] = {3, 1, 8, 6, 2, 7, 4, 5};
// 数组的大小
int size = sizeof(arr) / sizeof(arr[0]);
// 使用分治算法查找最大元素及其索引
struct MaxResult result = findMax(arr, 0, size - 1);
// 输出结果
printf("最大元素:%d,索引:%d\n", result.maxElement, result.maxIndex);
return 0;
}
1.1.6 回溯
回溯法也是枚举法的一种,它的特点就是在搜索过程中寻找问题的解,当发现不满足求解条件时就回溯(返回),尝试别的路径,避免无效搜索。
a) 题一
老鼠走迷宫,采用尝试错误的方法找到出口,在走错路时就退回来并把走过的路记下来,避免下次走重复的路,就这样找到出口为止。
老鼠需要遵守以下三个原则:
1、一次只能走一格。
2、遇到墙无法往前走则退回一步,寻找其它路。
3、走过的路不再走第二次。
使用二维数组代表地图,值为1则代表不能通行,值为0则代表可以通行。
假设老鼠从左上角[1][1]进入,从右下角[8][10]出来。
可以使用链表来记录走过的位置,并且将走过的位置所对应的数组元素内容标记为2,然后将这个位置放入堆栈,再进行下一个方向
或路的选择。如果走到死胡同并且还没有抵达终点,就退回到上一个位置,再选择其他的路。由于每次新加入的位置必定会在堆栈的
顶端,因此堆栈顶端指针所指向的方格编号就是当前老鼠的位置,如此重复直至走到迷宫出口为止。
思路:
回溯法通常使用栈实现。例如求解括号组合,图的深度优先遍历等。
解:
#include <stdio.h>
// 定义迷宫的大小
#define ROWS 8
#define COLS 10
// 迷宫地图,1表示墙,0表示通路
int maze[ROWS][COLS] = {
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 1, 0, 0, 0, 0, 1},
{1, 0, 1, 0, 1, 0, 1, 1, 0, 1},
{1, 0, 1, 0, 1, 0, 0, 1, 0, 1},
{1, 0, 1, 1, 1, 1, 1, 1, 0, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};
// 定义堆栈
int stack[ROWS * COLS][2];
int top = -1; // 堆栈顶端指针
// 打印迷宫路径
void printPath() {
for (int i = 0; i <= top; i++) {
printf("(%d, %d) -> ", stack[i][0], stack[i][1]);
}
printf("Exit\n");
}
// 回溯法解决老鼠走迷宫问题
int solveMaze(int startRow, int startCol, int endRow, int endCol) {
// 起点入栈
push(startRow, startCol);
maze[startRow][startCol] = 2; // 标记已经走过的位置
// 定义四个方向的移动
int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
while (!isEmpty()) {
int currentRow = stack[top][0];
int currentCol = stack[top][1];
// 到达终点
if (currentRow == endRow && currentCol == endCol) {
printPath();
return 1;
}
// 尝试向四个方向移动
int moved = 0;
for (int i = 0; i < 4; i++) {
int newRow = currentRow + directions[i][0];
int newCol = currentCol + directions[i][1];
// 判断新位置是否合法
if (maze[newRow][newCol] == 0) {
push(newRow, newCol);
maze[newRow][newCol] = 2; // 标记已经走过的位置
moved = 1;
break;
}
}
// 如果无法移动,回溯
if (!moved) {
pop();
}
}
// 无解
printf("No solution\n");
return 0;
}
int main() {
// 设置起点和终点
int startRow = 1, startCol = 1;
int endRow = 6, endCol = 8;
// 解决老鼠走迷宫问题
solveMaze(startRow, startCol, endRow, endCol);
return 0;
}
1.1.7 动态规划
动态规划法(Dynamic Programming Algorithm,DPA)类似于分治法,动态规划法的主要做法:
如果一个问题的答案与子问题相关,就能将大问题拆解成各个小问题,
其中与分治法最大的不同是可以让每一个子问题的答案被存储起来,以供下次求解时直接取用。
这样的做法不仅可以减少再次计算的时间,而且可以将这些解组合成大问题的解,可以解决重复计算的问题。
a) 题一
给定一个未排序的整数数组,找到最长递增子序列的长度。
思路:
定义状态: 定义一个状态数组 dp,其中 dp[i] 表示以第 i 个元素结尾的最长递增子序列的长度。
状态转移方程: 对于每个元素 nums[i],遍历其之前的元素 nums[j],如果 nums[i] > nums[j],则更新 dp[i] = max(dp[i], dp[j] + 1)。
最终结果: 返回 dp 数组中的最大值。
解:
#include <stdio.h>
// 动态规划法计算最长递增子序列的长度
int lengthOfLIS(int nums[], int size) {
if (size == 0) {
return 0;
}
// 初始化状态数组
int dp[size];// 注意,数组长度必须为常量,这里为了方便编写。实际可以通过malloc实现类似功能。
for (int i = 0; i < size; i++) {
dp[i] = 1; // 初始长度为1
}
// 动态规划状态转移
for (int i = 1; i < size; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = (dp[i] > dp[j] + 1) ? dp[i] : dp[j] + 1;
}
}
}
// 返回dp数组中的最大值
int maxLength = 1;
for (int i = 0; i < size; i++) {
maxLength = (maxLength > dp[i]) ? maxLength : dp[i];
}
return maxLength;
}
int main() {
// 示例数组
int nums[] = {10, 9, 2, 5, 3, 7, 101, 18};
// 数组的大小
int size = sizeof(nums) / sizeof(nums[0]);
// 使用动态规划法计算最长递增子序列的长度
int result = lengthOfLIS(nums, size);
// 输出结果
printf("最长递增子序列的长度为 %d\n", result);
return 0;
}
1.1.8 贪心
贪心法(Greed Method)又称贪婪算法,从某一起点开始,在每一个解决问题的步骤使用贪心原则,
即采用在当前状态下最有利或最优化的选择,不断地改进该解答,持续在每一个步骤中选择最佳的方法,
并且逐步逼近给定的目标,当达到某一个步骤不能再继续前进时,算法就停止,以尽可能快的方法求得更好的解。
a) 题一
有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。现在求需要几只箱子才能把这些物品都装起来。
解:
使用贪婪法求解该问题的基本思想是:先将物品的体积按从大到小的顺序排列。然后依次将物品放到它第一个能放进去的箱子中,若当前箱子装不下当前物品,则启用一个新的箱子装该物品,直到所有的物品都装入了箱子。如采用这种方式,我们发现,得到解决方案为:1、3号物品放一个箱子,2、4、5放第二个箱子,6放在第3个箱子,一共需要3个箱子。但由于此问题很简单,我们可以很容易用人工计算的方式得知最优解只要2个箱子。即:1、4、5和2、3、6。所以从此可以看出贪婪法求的是可行解,而非最优解。
#include <stdio.h>
#define NUM_ITEMS 6
#define BIN_CAPACITY 100
// 定义物品结构体
struct Item {
int index;
int volume;
};
// 比较函数,用于qsort排序
int compareItems(const void *a, const void *b) {
return ((struct Item *)b)->volume - ((struct Item *)a)->volume;
}
// 贪婪法求解函数
int greedyBinPacking(struct Item items[], int numItems) {
qsort(items, numItems, sizeof(struct Item), compareItems);
int bins = 0;
int binRemainingCapacity = BIN_CAPACITY;
for (int i = 0; i < numItems; ++i) {
if (binRemainingCapacity >= items[i].volume) {
printf("Item %d in Bin %d\n", items[i].index, bins + 1);
binRemainingCapacity -= items[i].volume;
} else {
bins++;
binRemainingCapacity = BIN_CAPACITY - items[i].volume;
printf("Item %d in Bin %d\n", items[i].index, bins + 1);
}
}
return bins + 1; // 返回箱子数量
}
int main() {
struct Item items[NUM_ITEMS] = {
{1, 60},
{2, 45},
{3, 35},
{4, 20},
{5, 20},
{6, 20}
};
int numBins = greedyBinPacking(items, NUM_ITEMS);
printf("Total bins needed: %d\n", numBins);
return 0;
}