栈的使用和基于堆栈的进制转换

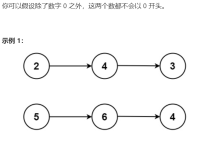
题目：

解答：

#include<stdio.h>
#include <stack>
#define MAXLEN 100 //MAXLEN最大长度 
std::stack <int>v;
typedef struct
{
	int data[MAXLEN];//定义char类型数组date[100] 
	int top;//定义标志 
}SeqStack;//声明栈结构体LinkStack

/*初始化顺序栈*/
void InitStack(SeqStack *S){
	S->top = -1;  //声明栈从0开始，最大元素99 
}
/*判断栈是否为空*/
int EmptyStack(SeqStack *S){
	if(S->top == -1)
	    return 1;
	else
	    return 0;
}
/*判断栈满*/
int FullStack(SeqStack *S){
	if(S->top == MAXLEN-1)
	    return 1;
	else
	    return 0;
}
/*进栈*/
int Push(SeqStack *S, int x){
	if(FullStack(S)){
		printf("栈满，不能进栈！\n");
		return 0;
	}
	else{
		S->top++;
		S->data[S->top]=x;
		return 1;
	}
}
/*出栈*/
int Pop(SeqStack *S, int *x){
	if(EmptyStack(S)){
		printf("栈空，不能出栈！\n");
		return 0;
	}
	else{
		*x = S->data[S->top];
		S->top--;
		return 1;
	}
}
/*取栈顶元素*/
int GetTop(SeqStack *S, int *x){
	if(EmptyStack(S)){
		printf("栈空，取栈顶元素失败！\n");
		return 0;
	}
	else{
		*x = S->data[S->top];
		return 1;
	}
}
/*进制转换*/
void Change(int n,int d){
	while(n)
    {
        v.push(n % d);
        n = n / d;
    }
    while(!v.empty())
    {
    	if(v.top()>=10)
    	printf("%c", v.top()+0x37);
    	else
		printf("%d", v.top());
        v.pop();///pop的返回值类型为空
    }
}
void Menu()
{
	    printf("\n       顺序栈的各种操作");
		printf("\n==========================================");
		printf("\n|      1--始化顺序栈                     |");
		printf("\n|      2--调用入栈函数                   |");
		printf("\n|      3--调用出栈函数                   |");
		printf("\n|      4--取栈顶元素                     |");
		printf("\n|      5--调用进制转换函数               |");
		printf("\n==========================================");	
		printf("\n请输入菜单号（0-5）：");
}
main(){
	int i,n,flag;
	SeqStack S;
	int x;
	char ch1,ch2,a;
	ch1 = 'y';
	while(ch1 == 'y' || ch1 == 'Y'){
		Menu();
		scanf(" %c",&ch2);
		getchar();
		switch(ch2){
			case '1':
				InitStack(&S);/*初始化顺序栈*/
				printf("栈的初始化完成！\n");
				break;
			case '2':
				printf("输入要入栈的元素个数：\n");
				scanf("%d",&n);
				printf("输入%d个入栈的字符：",n);
				for(i=0; i<n; i++){
					scanf(" %c",&x); 
					flag = Push(&S,x);/*进栈*/
				}
				if(flag == 1)
					printf("入栈成功！\n");
				break;
			case '3':
			    printf("输入要出栈的元素个数：\n");
			    scanf("%d",&n);
			    printf("出栈的元素为：\n");
			    for(i=0; i<n; i++){
			    	flag = Pop(&S,&x);
			    	printf("%c",x);
				}
				if(flag == 1)
				    printf("出栈成功！\n");
				else
				    printf("出栈失败！\n");
				break;
			case '4':
				if(flag = GetTop(&S, &x))
				    printf("当前的栈顶元素为%c\n",x);
				break;
			case '5':
				printf("请输入一个十进制数字：\n");
				scanf("%d",&n);
				printf("将这个十进制转换为几进制？");
				scanf("%d",&flag);
				Change(n,flag); 
				break;
			case '0':
				ch1 = 'n';
			    break;
			default:
				printf("输入有误，请输入0-5进行选择！\n");
		}
	}
}